|
Majid Mohammadian,
Ph.D., P.Eng. Associate Professor Department of Civil Engineering University of Ottawa 161 Louis Pasteur, CBY A114 ,Ottawa,
Ontario, Canada, K1N 6N5 Tel: (613) 562-5800-ext 6492, Fax:
(613) 562-5173 Email: majid.mohammadian@uOttawa.ca |
|
|
Research on Computational Fluid Dynamics (CFD) |
|
|
||
|
|||||
|
My research on numerical methods is geared towards developing efficient
and accurate methods for engineering problems related to Civil Engineering.
My research interests in this field include: |
|||||
|
1-
Numerical methods for shallow water flows with moving
boundaries 2-
Numerical methods for large scale oceanic and atmospheric
flows 3-
Numerical methods for coupled sediment –flow interactions 4-
Numerical methods for atmospheric boundary layer |
|||||
Numerical methods for shallow water flows with moving boundaries
Shallow water flows with moving boundaries exist in many natural situations
concerning rivers, lakes, estuaries and oceans. Dam-break flows, flood
propagation, tidal currents and river flows are examples for which shallow
water equations have proven accurate and reliable. Topographical (source) terms
in shallow water equations are of significant importance since they exist in
almost all engineering problems. Unstructured grids are of great interest in
solving real natural problems because of their capability of modelling complex
boundaries and local mesh refinement. Therefore, an unstructured finite-volume
method with a capability of modelling shallow waters with moving beds and
boundaries has substantial applications in management and improvement of water
resources.
Finite-volume (FV) methods are widely used in fluid dynamics because
they can easily solve complex flow regimes, including supercritical and transcritical currents. Moreover, they conserve both mass
and momentum, which is crucial for the correct calculation of complex flows
such as shock waves. However, they face some numerical problems in modelling of
source terms. This is because of imbalance issue between the source and flux
terms which could be very serious in real applications. In the past decade,
extensive research has been performed on balancing source and flux terms.
However, most existing schemes are computationally expensive, restricted to
structured grids or else they introduce a high level of numerical diffusion.
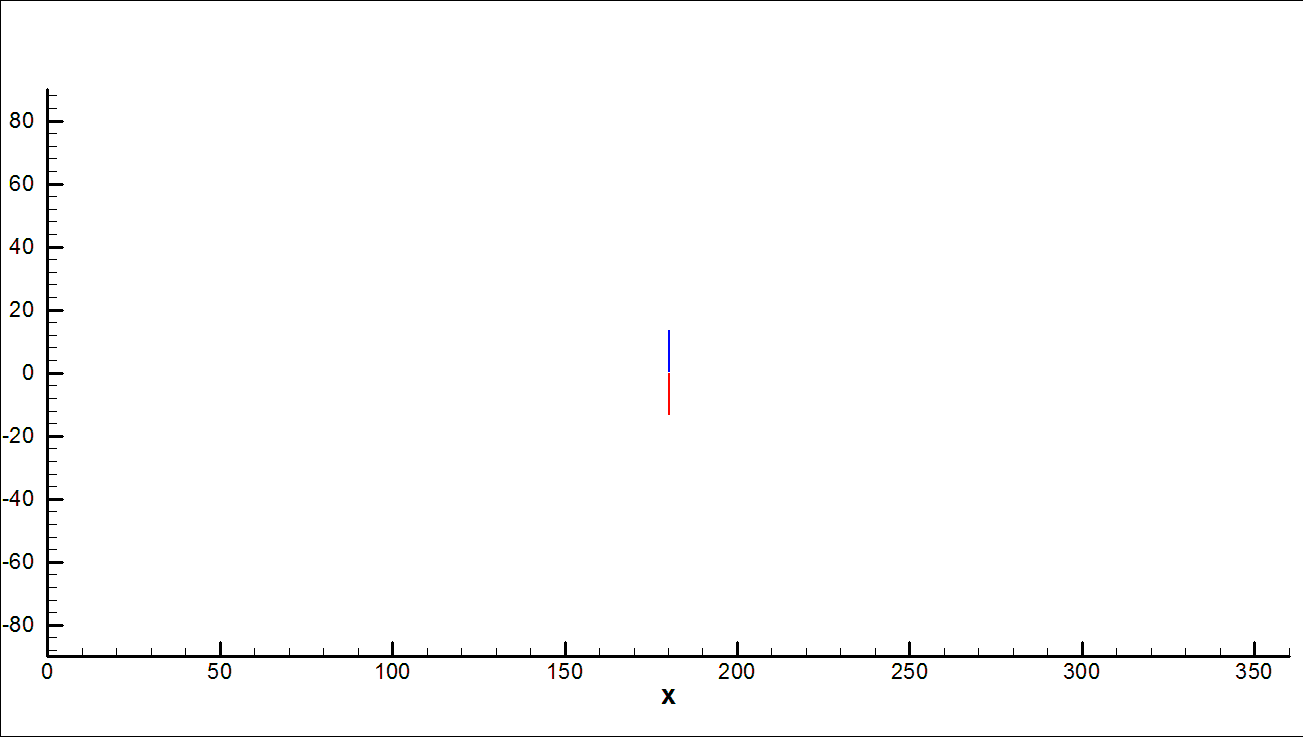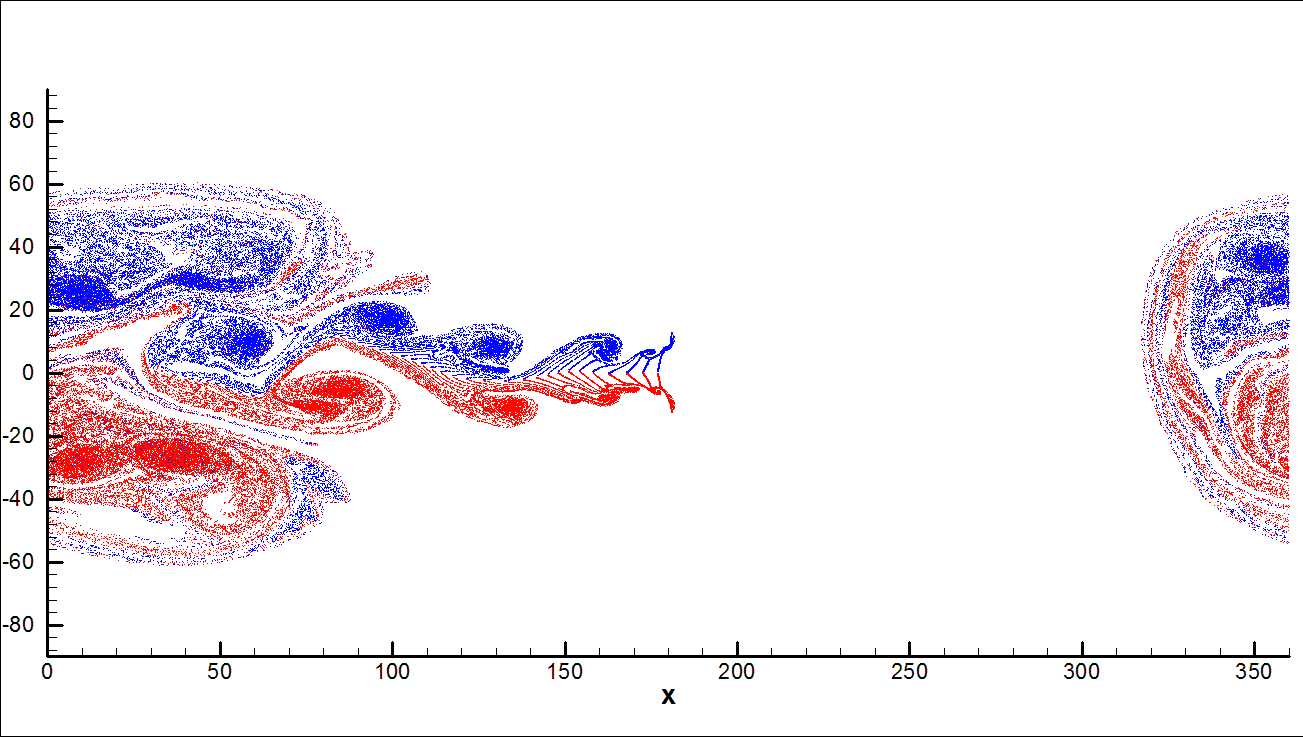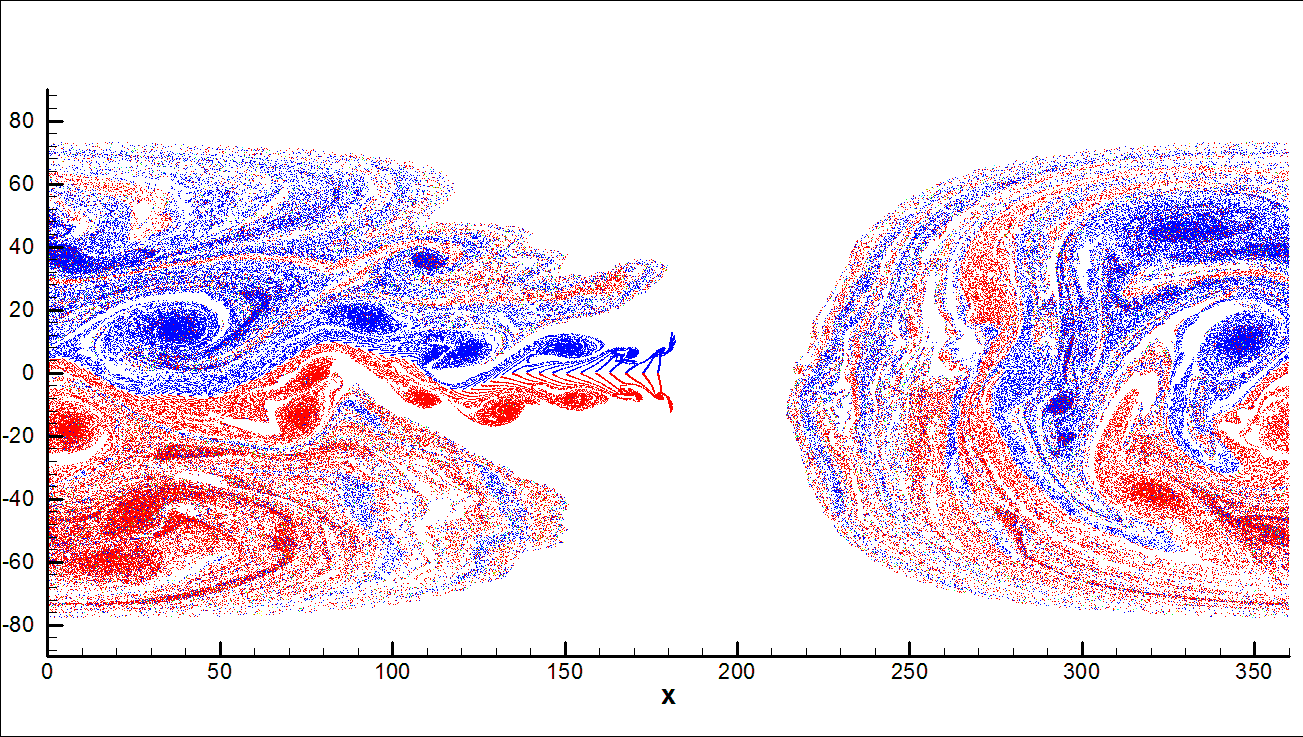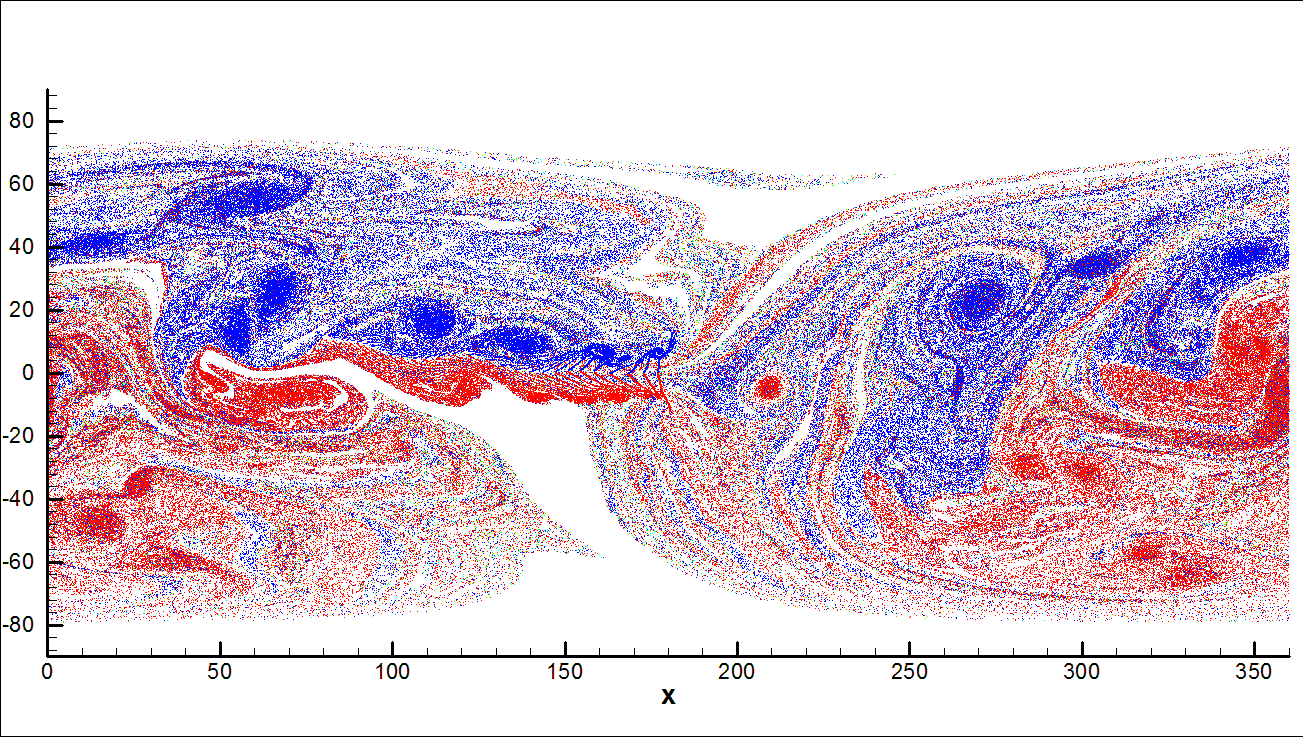
Numerical methods for large scale oceanic and atmospheric flows
In oceanic and atmospheric circulations, in addition to the convective
terms, the Coriolis effect
also plays an essential role in the flow pattern. Indeed, the shallow water
system allows for several waves, such as gravity, inertio-gravity,
and Rossby waves, which have completely different
structures. For example, the phase speeds of these waves are largely different;
gravity waves propagate with a relatively fast speed, while Rossby
waves are very slow.
Accurate simulation of all waves is a delicate problem for most
available schemes. In general, upwind schemes perform very well for gravity and
shock waves, but they are too diffusive for Rossby
waves. On the other hand, centered schemes perform better for slow modes such
as Rossby waves, but they present poor performance
for gravity and shock waves. The application of upwind schemes for
rotation-dominated cases still needs to be studied. For example, the phase
speed of Rossby waves and their damping due to
numerical schemes is an important issue in oceanic and atmospheric circulation
modeling. Indeed, most energy transfer in the ocean and atmosphere is performed
by Rossby waves. Therefore, damping of Rossby waves beyond a certain level is undesirable and
leads to erroneous results. On the other hand, in oceanic and atmospheric
circulations, small-scale and fast gravity waves are mainly considered as
noises which do not play an essential role in energy transfer and general
circulation. Therefore, in order to increase stability, it is usually desirable
to damp noises, which is perfectly done by upwind schemes. Thus, a desirable
scheme for the purpose of simulation of general circulation should present a
low level of damping of the Rossby waves, while
damping noises.
|
|
|
Numerical methods for coupled sediment & flow interactions
Intense sediment transport and rapid bed evolution are frequently
observed in rapidly varying flows, and bed erosion sometimes is of same magnitude
as flow. Simultaneous simulation of multiple physical processes requires a
fully coupled system to obtain an accurate hydraulic and morphodynamical
prediction. My research in this field is geared towards developing high-order
well-balanced fully coupled two-dimensional (2-D) mathematical models
consisting of flow and sediment transport equations based on finite-volume
methods. The 2-D shallow water system with friction terms is used as hydraulic
model and modified to take the effects of sediment exchange and bed level into
account on the wave propagation. A 2-D non-equilibrium sediment transport
equation is used to predict the sediment concentration variation. Since
bed-load, sediment entrainment and deposition all have significant effects on
bed evolution, an Exner-based equation is adopted
together with the Grass bed-load formula and sediment entrainment and
deposition models to calculate the morphological process. The resulting 5×5
hyperbolic system of balance laws leads to a challenging problem which requires
specifically designed numerical methods which are both efficient and accurate
and can be implemented over unstructured girds.
Numerical methods for
atmospheric boundary layer
Stability concerns are always a factor
in the numerical solution of nonlinear diffusion equations, which are a class
of equations widely applicable in different fields of science and engineering,
including atmospheric boundary layer. My research in this field is geared
toward developing efficient and accurate methods for the solution of nonlinear
diffusion equations, with a special focus on the atmospheric boundary layer diffusion
process. “Optimal schemes” are sought using various techniques such as the
development of low-diffusive and low-dispersive numerical methods which remain
stable for large time steps. Development
of numerical filters is also an approach that we follow. We have developed
Optimal Diagonally implicit Runge Kutta
(DIRK) methods and Total Variation Diminishing (TVD) schemes which have proved
to be useful for atmospheric boundary layers and the results have been
published in various journals including JCP. This research is supported by
Environment Canada for the Canadian whether prediction model.
Numerical methods for Advection-Diffusion
equations
Advection-Diffusion equations arise in
various problems including pollutant transport in water resources and
atmospheric flows. My research in this field aims at developing optimally
stable, accurate, and low diffusive/ low dispersive schemes using various
techniques such as Implicit-Explicit Runge-Kutta
methods (IMEX).
A lot of systems of equations in Civil Engineering are of the type
hyperbolic, such as shallow water equations, Euler system, sediment transport
equations, advection equations, etc. My research in this field aims at
developing accurate methods with certain properties such as well-balanced
property in complex planar or spherical geometries using structured or
unstructured grids.