CHG 3316

 

   TRANSPORT PHENOMENA

 

Assignment #6

 

 

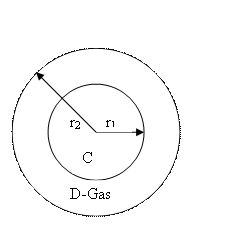
10-2. A droplet of material C (radius r1) is suspended in a gas stream of D which forms a stagnant film around the droplet (radius r2). If the C concentrations are xc1 and xc2 at r1 and r2, find the flux of C.

 

Droplet

 

 

At r = r1,  x = xc1

                 r = r2,  x = xc2
 

 

SOLUTION

 

Let Dcd be the diffusion coefficient.

 

ASSUMPTIONS

 

  1. One dimensional Diffusion (in the r-direction only)
  2. Steady state
  3. No reaction nor generation is taking place.

 

Based on the assumptions, equation 10-9 (Griskey) for cylindrical co-ordinates, becomes:

 

 

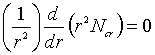
………………(1)

 

= /…………….(2)

 

From equation (10-6, Griskey) we have the definition of the flux:

 

But =0 (Stagnant film)

 

 

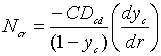…………..(3)

Substituting (1) in (3), we will obtain:

 

 

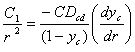
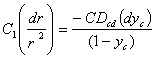…………….(4)

BOUNDARY CONDITIONS

 

At r = r1, yc = xc1

       r = r2, yc = xc2       ,     and by the Integration of Eq(4) above:

 

 

() =

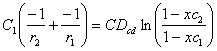
() =   and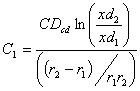

 

From (2), we have

 

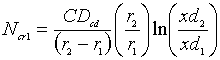                (Solution for the flux)

 

10-4. An industrial pipeline containing ammonia gas is vented to the atmosphere (a 3 mm tube is inserted into the pipe and extends for 20 m into air). If the system is at 25oC, find the mass rate of ammonia lost from the vent.

 

SOLUTION

 

With the following data available:

 

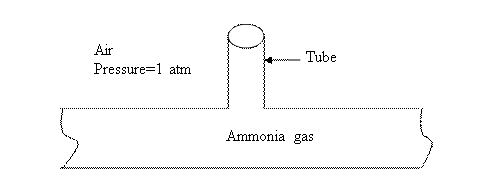
For the tube, Diameter, D=3 mm

 

                      Length, L=20 m

 

Temperature of system, T=25oC.

 

Diffusivity of Ammonia gas in tube,

 

Molecular weight of Ammonia=17.03 g/mol

 

Molecular weight of Air=28.97 g/mol

 

Assume that Ammonia gas is diffusing in the y-direction only.

 

ASSUMPTIONS

  1. One dimensional diffusion (y-direction)
  2. Steady state
  3. No reaction nor generation occurs

 

 

Based on the assumptions above, equation (10-7, Griskey) for rectangular co-ordinates becomes:

 

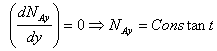……(1)

 

And the definition of flux, from equation (10-6, Griskey) for rectangular co-ordinates,

 

 

=0 as there is no bulk flow.

………………..(2)

 

Integrate the above equation ( EQ 2)  with boundary conditions.

 

BOUNDARY CONDITIONS

 

At L=0, CA=CAO 

 

        L=20 m, CA=CAL

 

……..(3)

 

From ideal gas law, CA=P/RT

 

 

Substituting in (3),

 

 

We have

 

 

Mass flow rate of Ammonia lost from Vent,

 

Where MA is the molecular weight of Ammonia

            A is the area of the tube.

 

10-9

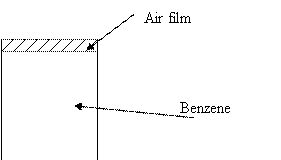
Benzene at 22°C is open to the atmosphere in a circular tank (6.10 m in diameter). Vapor pressure and specific gravity for benzene are 0.132 atm and 0.88. An air film of 5-mm thickness is above the benzene. What is the cost of evaporated benzene per day (assume value of benzene is $2 per gallon)?

 

 

 

 

 

 

 

 

 

 


Given Data:

 

Benzene Temperature = 22 C

Vapour pressure of Benzene = 0.132 atm

Specific gravity = 0.88

Air film of thickness = 5mm

Diameter of tank = 6.10 m

Cost of benzene = $ 2 per gallon

 

 

 

ASSUMPTIONS

 

 

·        Diffusion of A molecules (Benzene) is only in one direction i.e. in the z direction no flux in x and y direction

·        Steady state  with no chemical reaction i.e.

·        The air film above can be assumed to be a stagnant layer of B molecules(non diffusing)

 

 

In this case, the system is a liquid A (benzene) evaporating into Gas B (air) i.e. diffusion through a stagnant gas film model.

 

Apply the above assumptions to the equation of continuity of species for rectangular coordinates (Equation 10-7 Griskey):

 

 


 

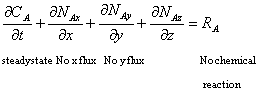
To obtain:

 

   

 

Therefore   is independent of z i.e. it is a constant

 

Then, using the Fick’s definition of flux NA (Equation 10-6 Griskey):

 


 

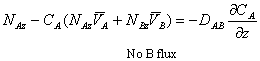
The equation above can be rearranged to get:

 

                         

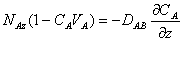
We can substitute the concentration term on the left side of the above equation with the mole fraction YA to get:

 

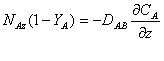                   ……    (1)

knowing

 

 

Replace the above equation into equation 1, we can derive the molar flux of A molecule in term of mole fraction YA:

 

 

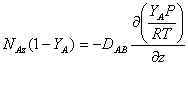
Since P, R and T are constant, they can be factored out of the derivative to obtain:

 

                            ,,,,,,, (2)

 

 

BOUNDARY CONDITIONS

 

z =z1               YA= YA1

z =z2               YA= YA2

 

The equation obtained above (equation 2) can be integrated as follows (since NAz is constant):

 

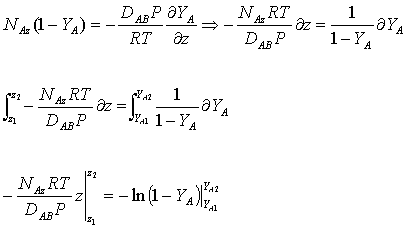
    ,,,,,,,,(3)

 

Letting  (thickness) and rearranging the equation above we obtain:

 

                  ,,,,,,,,,,,,,(4)

 

The above equation of flux (Equation 4) can be written in terms of mole fraction for the stationary molecule i.e. YB as follows:

 

                                     ,,,,,,,(5)

 

At the surface of benzene liquid:

 

The vapour pressure of benzene = 0.132 atm therefore:

=0.132 and

 

Assuming all the benzene is swept away by moving molecules of air above the stagnant air film i.e. the concentration of benzene above the air film is negligible, then:

 

 

 

Since the diffusivity of benzene is not given, it can be calculated from the following equation:

 

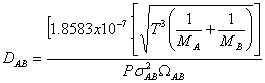
From A-3-3 in Griskey:

 

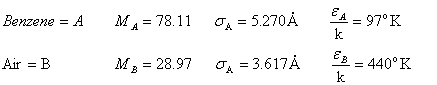
 And,

 

 

 

To obtain, table A-3-4 can be used using:

 

 

 

 

Therefore the diffusivity is:

 

 

 

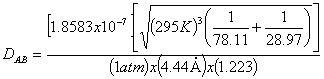
Now that we have all the parameters needed to determine the molar flux of benzene, we can substitute the above parameters into the molar flux equation derived earlier:

 

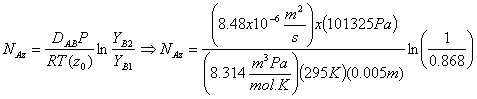
From the molar flux, the amount of benzene in gmols/sec can be determined as follows:

 

 

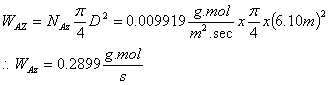
The amount of benzene evaporated per day:

 

=

 

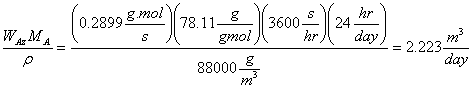
 Gallons of benzene evaporated in one day:

 

 

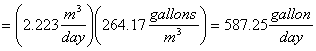
Therefore the Cost of benzene evaporated per day:

Cost of benzene evaporated =