Answers for Assignment 7

Problem 10-20: An alcohol and water vapor mixture is being separated by contact with an alcohol-water liquid solution. Alcohol is transferred from gas to liquid, and water is transferred from liquid to gas. Temperature and pressure are 25°C and 1 atm. The components diffuse through a gas film 0.1 mm thick at equal flow rates. Mole percents of alcohol are 80 and 10 on either side of the film. Find the rate of diffusion of both components through a film area of 10 m².

Consider this to be a case of equimolar counter diffusion we did in the class:

We start from the modified equation 10-6:

Since we have equimolar counter diffusion: N_A = - N_B

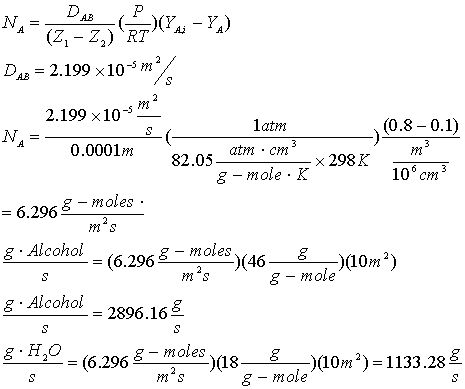
Problem 10-39: Oxygen is transferred from the inside of the lung through the lung tissue to blood vessels. Assume the lung tissue to be a plane wall of thickness L and that inhalation maintains a constant oxygen molar concentration at the inner wall as well as another constant oxygen molar concentration at the outer wall. Additionally, oxygen is consumed in the lung tissue by a metabolic reaction (zeroth order). Determine the distribution of oxygen in the tissue and the rate of assimilation of oxygen by the blood.

Solution:

In this case there is no bulk flow to be considered since we are dealing with membrane and negligible concentration of Oxygen within the membrane (i.e.: Y_A is very small in modified Equation 10-6. Also we have zeroth order reaction rate (R_A=k₀). Thus, at steady state, equation 10.7 simplifies to:

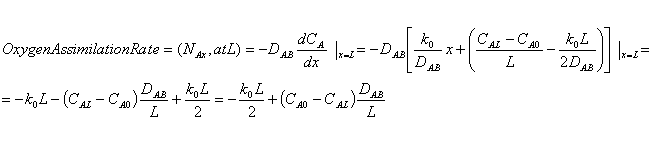
Problem 10-40: Carbonization of steel is a high-temperature process. At a temperature of 1273 ºK, how much time would be required to raise the steel carbon content at a depth of 1 mm from 0.1 to 1.0 percent (carbon mole fraction on steel surface is 0.02)? Take D_AB = 3.17 x 10^-11 m²/s.

y = 1 mm = 0.001m

3.17 x 10^-11 m²/s

x₀ = 0.02

x₁ = 0.001

x₂ = 0.01

To use Figure 4.1-2 use C/C₀ instead of v_x/V and D_AB instead of υ.

Then and

Since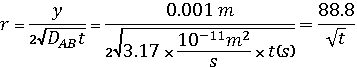

From the Unsteady –State Figure 4.1-2 given in the class for rectangular Momentum Transfer for n=1:

à r₁ = 1.35 and = 0.5 à r₂ = 0.48

and

Total time = 34225 – 4327 = 29898 sec = 8.3 hours

Problem 4: Hydrogen gas (27°C; 10 bars) is stored in a 100-mm-diameter spherical tank (2mm-thick wall). Molar concentrations of hydrogen at the inner and outer wall are 1.5 kg-mole/m³ and 0, respectively. Diffusivity of hydrogen in steel is 0.3x10^-12 m²/sec. Find the rate of hydrogen loss through the wall as well as the rate of pressure drop in the tank at steady state. Because of the high ratio of the diameter of the sphere to the thickness of the steel wall, do the same calculations, assuming rectangular geometry for the 2 mm. thick steel wall the hydrogen is leaking through and calculate the % error for making this assumption.

For Spherical:

Starting from modified equation 10.6:

In this case there is no bulk diffusion to be considered since we are dealing with membrane and negligible concentration of hydrogen within the membrane. Thus, equation 10.6 simplifies to:

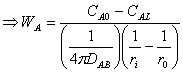
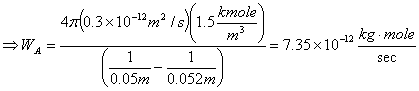
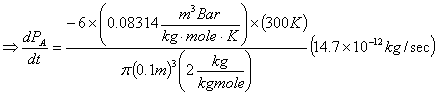
For Rectangular:

Starting from the modified equation 10.6 for binary system, again:

In this case there is no bulk flow to be considered since we are dealing with membrane and negligible concentration of hydrogen within the membrane. Thus, modified equation 10.6 simplifies to:

_{From equation 10-7 for a rectangular system, NA=constant, so we can integrate the above equation:}

Surface area of leak can be taken as the same as the sphere: 4πr² = 4π(0.1/2)²m² = 0.0314m²

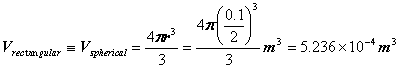
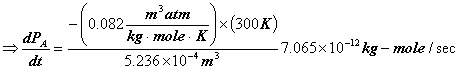
Assume 1 bar = 1 atm.

% error for hydrogen loss rate

% error for pressure drop rate