Work of Catherine Mavriplis in
Numerical Methods and Computational Fluid Dynamics

Catherine Mavriplis was trained as a fluid dynamicist and numerical fluid dynamicist, starting with an undergraduate thesis in finite difference methods for fluid flow and thermal convection, an aerodynamics panel method at the National Research Council of Canada, and then spectral, finite difference, finite volume, finite element, boundary element and spectral element methods at MIT. Her PhD thesis concentrated on the ingredients for making the spectral element method adaptive. The adaptive method has proven itself in fluid dynamics and combustion (see publications and results below). Dr. Mavriplis has used her computational skills in a number of traditional and interdisciplinary areas: aerodynamics, transitional flows, combustion, MEMS, magnetic refrigeration, propulsion, and most recently meteorology. 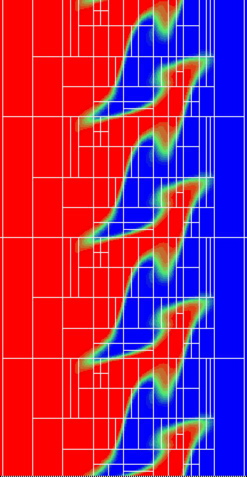An example of a simulation by the adaptive spectral element method is shown here. This simulation of the temperature field for a premixed flame front wrinkled by a velocity field with shear and arrays of vortices was obtained by the adaptive method developed by Mavriplis and her student Huiyu Feng. Starting with an initial grid of 12 elements and 5th order polynomials, the adaptive method (for the solution shown here) employs 200 elements (outlined in white) with elemental approximating polynomials of degrees ranging from 5 to 13. The overhead time spent in adaptivity is less than 1% of the total CPU time and the savings over a non-adaptive method are 50%.