La recherche de Catherine Mavriplis en
méthodes numériques et dynamique des fluides numérique

Catherine Mavriplis a suivi une éducation en dynamique des fluides et méthodes numériques débutant avec une thèse de 1er cycle en méthodes de différences finies pour écoulements fluides avec convection de chaleur, ensuite un stage au Centre National de Recherche du Canada travaillant sur les méthodes dites 'panel' en aérodynamique, puis à travers sa recherche de maîtrise et de doctorat au MIT sur les méthodes spectrales, volumes finis, éléments finis, 'boundary element' et éléments spectraux. Sa thèse de doctorat concerne les éléments mortiers ('mortar') et les estimateurs d'erreurs pour l'adaptivité de la méthode d'éléments spectraux pour simulation directe d'écoulements. Ses compétences numériques et d'analyse se sont avérées utiles dans un certain nombre de projets dont plusieurs qui sont interdisciplinaires: aérodynamique, transition à la turbulence, combustion, MEMS, refrigération magnétique, propulsion et météorologie. 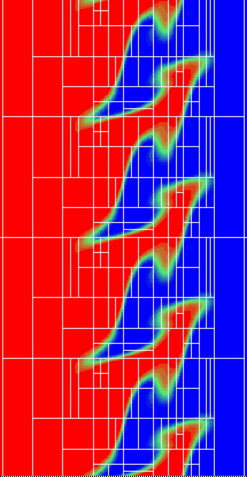Un exemple de simulation par la méthode adaptative d'éléments spectraux est illustrée ici. Cette simulation de distribution de température pour un front de flamme prémélangée froissée par un champ de vitesse avec cisaillement et tourbillons fut obtenue par la méthode adaptative d'éléments spectraux développée par Prof. Mavriplis et son étudiante Huiyu Feng. Commençant le calcul avec un maillage de 12 éléments et des polynômes d'ordre 5, la méthode adaptative emploie (pour ce cas) 200 éléments (cernés en blanc) avec des polynômes d'ordres variés de 5 à 13. L'adaptivité prendrait 1% du temps total du calcul et le temps de calcul est réduit de 50%.